To understand the Fourier series consider a more general problem, where a periodic signal x(t), of period
Question:
To understand the Fourier series consider a more general problem, where a periodic signal x(t), of period T0, is approximated as a finite sum of terms
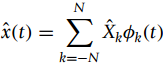
where {?k (t)} are ortho-normal functions. To pose the problem as an optimization problem, consider the square error
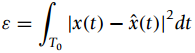
and we look for the coefficients {X?(k)}that minimize ?.
(a) Assume that x(t) as well as x?(t) are real valued, and that x(t) is even so that the Fourier series coefficients Xk are real. Show that the error can be expressed as
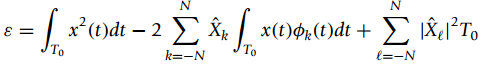
(b) Compute the derivative of ? with respect to X?n and set it to zero to minimize the error. Find X?n.
(c)?In the Fourier series the {?k(t)} are the complex exponentials and the {X?n} coincide with the Fourier series coefficients. To illustrate the above procedure consider the case of the pulse signal x(t), of period T0 = 1 and a period
x1(t) = 2[u(t + 0.25) ? u(t ? 0.25)]
Use MATLAB to compute and plot the approximation x?(t) and the error ? for increasing values of N from 1to 100.
(d) Concentrate your plot of x?(t) around one of the discontinuities, and observe the Gibb?s phenomenon. Does it disappear when N is very large? Plot x?(t) around the discontinuity for N = 1000.
Step by Step Answer:
Assuming xt and xt being real and even so that X k are real we have To minimi...View the full answer
