We are given a noisy signal

x(t) = s(t) + η(t)

where s(t) is the desired signal and η(t) is additive noise. From experience, we know that the average power of the desired signal and the noise has finite support. That is

|S(f)|² = 0  f ‰¥ 10 kHz

|N(f)|² = 0   f ‰¥ 20 kHz

where S(f) and N(f) are the Fourier transforms of s(t) and η(t) in terms  of the frequency f(see top figure in Figure 10.19). Suppose we use the  system shown at the bottom of Figure 10.19 to process x(t)to make  it €œlook better,€ i.e., reduce the effects of the noise without distorting  the desired signal.

We have four second order filters (A to D) to choose from. The gain  K = 0.25 for each and the poles {p_i} and zeros {z_i} are

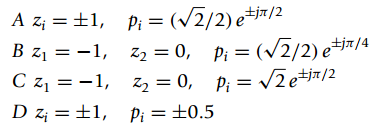
where i =1, 2.

(a) Suppose that for hardware reasons the sampling rate f_s you can  use is limited to 10, 20, 30, 40, or 50 kHz. Select f_s from those  available and explain the reason for your choice.

(b) Select an appropriate filter from those available and explain the  reason for your choice.

(c) Determine H(z) = KN(z)/D(z) for the filter of your choice, where  N(z) and D(z) are polynomial in z with real coefficients.

(d) Determine and sketch |H(e^jω)|, for €“Ï€ ‰¤ ω ‰¤ Ï€. Evaluate carefully  the values at ω = 0, ±Ï€.

Figure 10.19:

A z; = ±1, Pi = (/2/2) e+i*/2 B z1 = -1, z2 = 0, P; = (/2/2) e*i™/4 C z1 = -1, z, = 0, p; = /2e#j™/2 D z; =±1, Pi = ±0.5 |S(S)? |N()P f (KHz) 10 r[n] y/n] H(2) x(t) y(t) Sampler Ideal D/A f.