MgF 2 adopts the rutile structure (Figure 1.45) with a = 4.62 and c = 3.04 . The bondvalence parameter R0 MgF = 1.581

MgF₂ adopts the rutile structure (Figure 1.45) with a = 4.62 Å and c = 3.04 Å. The bondvalence parameter R0 MgF = 1.581 Å.

(a) Use the bond-valence method to predict the length of the Mg–F bonds.

(b) Use the Born–Mayer equation to estimate the latticeformation energy for MgF₂.

(c) Comment on the difference between this value and the value of −2978 kJ/mol obtained from a Born–Haber cycle. Is the agreement between calculated and experimental values similar to that observed for the alkali-metal halides?

(d) Would you expect the lattice-formation energy of rutile (TiO₂) to be lower (more stable) than MgF₂?

Figure 1.45

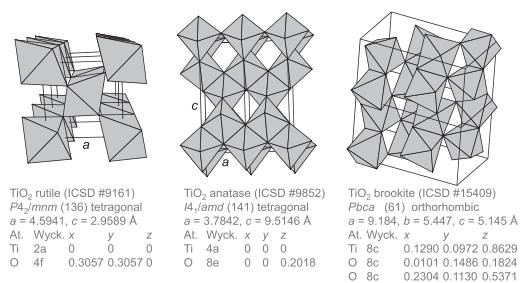
a TiO rutile (ICSD # 9161) P4 /mnm (136) tetragonal a = 4.5941, c = 2.9589 A At. Wyck. x y Ti 2a 0 0 0 4f 0.3057 0.3057 0 FO Z a TiO anatase (ICSD #9852) 14,/amd (141) tetragonal a = 3.7842, c = 9.5146 A At. Wyck. x y z 000 Ti 4a 08e 0 0 0.2018 TiO brookite (ICSD #15409) Pbca (61) orthorhombic a = 9.184, b= 5.447, c= 5.145 A At. Wyck. x y Z Ti 8c O 8c O 8c 0.1290 0.0972 0.8629 0.0101 0.1486 0.1824 0.2304 0.1130 0.5371