(a) Show that in the case of two identical atoms, the eigenstates of the LCAO model are the symmetric and antisymmetric linear combinations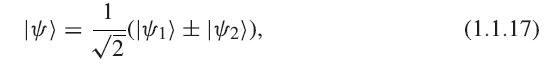

where the plus sign corresponds to the bonding state and the negative sign corresponds to the antibonding state. To simplify the problem, assume U₁₂ is real.

(b) The energies computed in (1.1.12) should actually be corrected slightly, because the change of the normalization of the wave function has not been taken into account. To account for the normalization, one should write 

where |²² is the full eigenstate. Determine this corrected energy for the bonding and antibonding states of two identical atoms.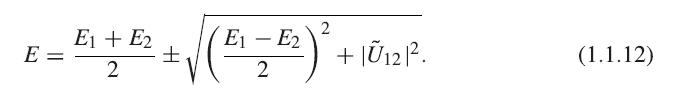

(c) If you did Exercise 1.1.1, then you can do a follow-up calculation to see how well the LCAO approximation works. Instead of a symmetric set of coupled wells, find the solution for the wave function of an electron in a single quantum well with an infinite barrier on one side and a barrier of infinite thickness, with height U₀, on the other side. Use this solution as the “atomic” state, and form symmetric and antisymmetric linear combinations of this. Determine the energies of the two states for 2mU₀/h̄² = 100 and a = 1, as the value of b is varied from 0 to 1. How well does the LCAO solution approximate the full solution? How important is the correction of part (b)?

Transcribed Image Text:

= 1 下 =(1) ±42), (1.1.17)