As a follow-up to Exercise 1.4.6, show that the special point at which the gap energy goes to zero in (1.9.19) for the graphene lattice is one of the corners of the Wigner–Seitz cell for the Brillouin zone in reciprocal space.

Data from Exercise 1.4.6:

A graphene lattice, or “honeycomb” lattice, is the same as the graphite lattice (see Table 1.1) but consists of only a two-dimensional sheet with lattice vectors

and a two-atom basis including only the graphite basis vectors in the z = 0 plane. Show that the reciprocal lattice vectors of this lattice are

Make a drawing of both the real-space and reciprocal-space lattices, and draw the Brillouin zone on the reciprocal space lattice.

Show that the structure factor for the two-atom basis multiplies the peak in reciprocal space at

and the peak at

Label the reciprocal lattice vectors on your drawing by their peak height and show that the reciprocal lattice has the same symmetry as the real-space honeycomb lattice, and is not a simple hexagonal lattice.

Show that the reciprocal lattice of graphene can be viewed as a simple hexagonal lattice with primitive vectors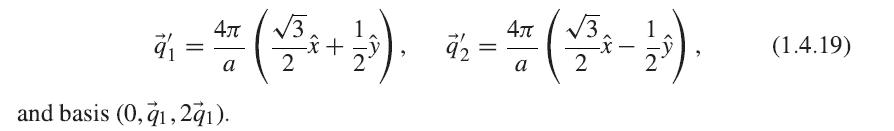

Show that the reciprocal lattice of this reciprocal lattice is a simple hexagonal lattice in real space with primitive vectors

Last, show that the structure factor of the reciprocal lattice in (c) eliminates one of every three real-space lattice points from the lattice of (d), leaving the original honeycomb lattice.

Transcribed Image Text:

En(K) = Eo ± U12√3+ 4 cos √3kx 2 COS ky - 2 + 2 cos ky. (1.9.19)