Find the first gap energy at ka = using (1.2.6) in the limit b 0
Question:
Find the first gap energy at ka = π using (1.2.6) in the limit b → 0 and U0b is small. You should write approximations for sinKa and cos Ka near Ka = π, that is, Ka ≃ π + (ΔK)a, where ±K is small. You should find that you get an equation in terms of K that is factorizable into two terms that can equal zero. The difference between the energies E = h̄2K2/2m for these two solutions for K is the energy gap.
Do your zero-point energy and gap energy vanish in the limit U0b → 0?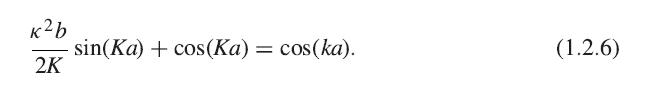
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





