In a cubic crystal, a triply degenerate band with p-symmetry has the following deformation Hamiltonian, known as the Pikus–Bir Hamiltonian (derived in Section 6.11.2):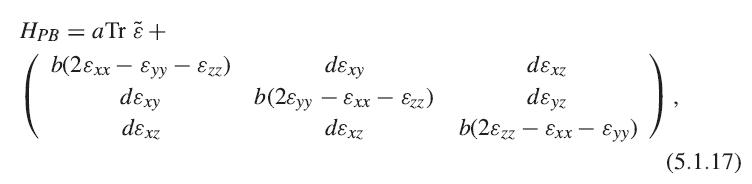

operating on the basis of the three degenerate states |p_x〉, |p_y〉, and |p_z〉. The constant a is a hydrostatic deformation potential, while b and d are shear deformation potentials.

(a) Show that for a uniaxial strain along the [001] direction, the hydrostatic shift is 3aε, where ε = 1/3 (ε_xx +ε_yy + ε_zz) is the hydrostatic strain, and the splitting of the states is equal to |3bτ |, where τ = ( 1/2 ε_xx + 1/2ε_yy − ε_zz). For a uniaxial strain along the [111] direction, show that the splitting of the states is equal to |3dτ|, where τ is the shear strain in this direction.

(b) Construct the shear deformation operator D̃ for the Pikus–Bir Hamiltonian above explicitly for the transverse phonon case

and show that the Hamiltonian in this case gives a nonzero electron–phonon interaction energy. Do the same for the transverse phonon along [110],

Show that this shear term also gives a nonzero contribution for longitudinal phonons.

Transcribed Image Text:

HPB = a Tr & + b(2Exx-Eyy dexy dɛxz Ezz) dɛxy b(2ɛyy - Exx - Ezz) dɛxz dɛxz dɛyz b(28zz Exx- Eyy) (5.1.17)