Prove the statements (10.2.7) and (10.2.8), and that the other terms vanish as stated, by explicitly evaluating

Question:

Prove the statements (10.2.7) and (10.2.8), and that the other terms vanish as stated, by explicitly evaluating the matrix elements, using the band functions in (1.13.9) and (1.13.10), and substituting Φ_x = x, Φ_y = y, Φ_z = z, and Φ_s = 1.

Show also that the term α_n is real for these states, because the factor i that appears in (10.2.9) cancels an i that occurs in the matrix elements.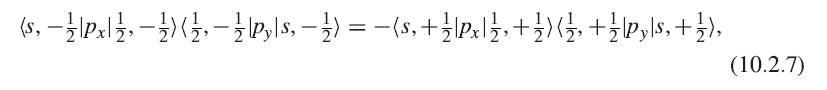

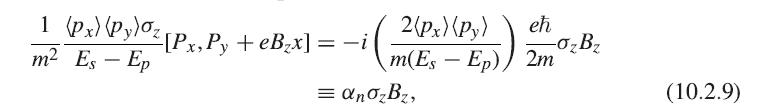
Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

Solid State Physics Essential Concepts

ISBN: 9781107191983

2nd Edition

Authors: David W. Snoke

See More Books

Question Posted: Aug 20, 2023 08:09 AM

See More Questions

The following additional information is available for the Dr. Ivan and Irene Incisor family from Chapters 1-5. Ivan's grandfather died and left a portfolio of municipal bonds. In 2012, they pay Ivan...
List three specific parts of the Case Guide, Objectives and Strategy Section (See below) that you had the most difficulty understanding. Describe your current understanding of these parts. Provide...
Managing Scope Changes Case Study Scope changes on a project can occur regardless of how well the project is planned or executed. Scope changes can be the result of something that was omitted during...
Copper Products Limited leases property on which copper has been discovered. The lease provides for an immediate payment of $472,000 to the lessor before drilling has begun and an annual rental of...
Mayfair Department Stores, Inc., operates over 30 retail stores in the Pacific Northwest. Prior to 2011, the company used the FIFO method to value its inventory. In 2011, Mayfair decided to switch to...
To what extent could a management auditor base the evaluation of economy and efficiency or effectiveness upon statistics obtained from the published financial statements of similar companies?
1 a) In cross-cultural business negotiations, nonverbal signals give insights into the attitudes and priorities of the participants. Expand the argument, using appropriate examples. b) How can a...
1. Why do you think so many American citizens and lawmakers reacted negatively to Googles decision in 2006? 2. Does the fact that Google is an Internet company change societal expectations of it...
What is the difference between a fixed cost and a variable cost and why are both of these costs important to the accounting process?
The Ising model can easily be solved numerically, if you are familiar with a basic programming language. Create an array or matrix s i , i = 1, . . . , N, which can have value either 1 or 1. The...
Imagine doing a two-slit interference experiment with electrons that go through two separate tubes (with no inelastic dephasing), as illustrated in Figure 9.23. The source emits wave packets that are...
What is the output of the following code? b = 3; while(b < 6) System.out.print(b + " "); a. 3 b. 3 4 5 c. 3 4 5 6 d. 3 3 3 3 3 3
Test - LOG 2060 Intermediate Systems Sustainment Management T07.E02 Describe DoD's Depot Maintenance Enterprise and How Core, 50-50, and Partnering Initiatives Question 30 of 31. In depot...
Assuming that StickerGiant plans to expand its business to overseas markets, what are the top 3 environmental factors (economic, political/legal, demographic, social, competitive, global, and...
Selina is an avid sky diver. How would an insurer rate the severity/probability of the risks to which Selina is exposed? a) minor/low b) critical/high c) material/medium d) critical/low
Primare Corporation has provided the following data concerning last month's manufacturing operations. Purchases of raw materials Indirect materials used in production Direct labor Manufacturing...
Perpendicular Offset Practice Problem Find the perpendicular offset and station of Point K relative to line JL. Point K N 2423.58 Point L. Point J N 2537.19 N 2399.34 E 1774.94 E 2223.41 E 2445.15
1. Which type of conflict is depicted in this scenario? 2. Evaluate Rande's approach to resolving this conflict. What conflict management style did she use: avoiding, accommodating, forcing,...
Where are the olfactory sensory neurons, and why is that site poorly suited for their job?
Consider the following substitution reaction: a) Determine whether this reaction proceeds via an S N 1 or S N 2 process. b) Draw the mechanism of this reaction. c) What is the rate equation of this...
Consider the structures of 2-nitrophenol and 3-nitrophenol. These compounds have very different pKa values. Predict which one has the lower pK a , and explain why. (In order to solve this problem,...
Draw a Lewis structure for each of the compounds below: a) CH 2 = CHOCH 2 CH(CH 3 ) 2 b) (CH 3 CH 2 ) 2 CHCH 2 CH 2 OH c) (CH 3 CH 2 ) 3 COH d) (CH 3 ) 2 C = CHCH 2 CH 3 e) CH 2 = CHCH 2 OCH 2 CH(CH...
Flexible manufacturing places new demands on the management accounting information system and how performance is evaluated. In response, a company should a. institute practices that reduce switching...
Revenue and expense items and components of other comprehensive income can be reported in the statement of shareholders' equity using: U.S. GAAP. IFRS. Both U.S. GAAP and IFRS. Neither U.S. GAAP nor...
Kirk and Spock formed the Enterprise Company in 2010 as equal owners. Kirk contributed land held an investment ($50,000 basis; $100,000 FMV), and Spock contributed $100,000 cash. The land was used in...

Prove the statements (10.2.7) and (10.2.8), and that the other terms vanish as stated, by explicitly evaluating

Question:

<호, +를pyls, +호), (10.2.7)

Step by Step Answer:

The states from Section 113 are in the notation of Section 102 12x ilyt 12 1x iy 2z x iy 2z 12x iy4 ...View the full answer

Solid State Physics Essential Concepts

Students also viewed these Sciences questions