The Ising model can easily be solved numerically, if you are familiar with a basic programming language. Create an array or matrix s_i, i = 1, . . . , N, which can have value either 1 or −1. The initial values can be picked randomly. The array is updated by the following algorithm: 

(1) For each site in the array, calculate the interaction energy

for each possible spin value s_i = ±1 based on the average of the nearest neighbors.

(2) Set si to a new value, either spin +1 or −1, with probability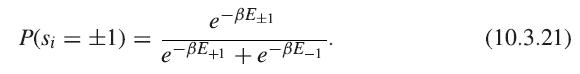

(3) After updating the whole array, start over and continue to iterate the updating process until it converges to having the same average properties.

Show that for a one-dimensional system, the average value of m increases as T decreases, without any sharp transition, while for a two-dimensional system, there is a critical temperature at which the average spin jumps up, which depends on your choice of J.

Ei ; = -1 sis; j (10.3.20)