Question: Show that a symmetry operator R must be unitary, that is, its adjoint is equal to its inverse; for a matrix representation this means that

Show that a symmetry operator R must be unitary, that is, its adjoint is equal to its inverse; for a matrix representation this means that its inverse is equal to the complex conjugate of the transposed matrix. There are several steps to showing this.

(a) Show that

(b) Inserting a sum over a complete set of states into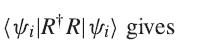

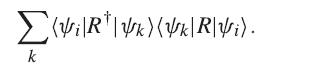
By evaluating this, show that

and therefore R is unitary. Note that this analysis also implies that only one row in any column is nonzero, and vice versa.

|ij | = 1.

Step by Step Solution

★★★★★

3.42 Rating (165 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a First we need to establish that laj2 1 Note that since as established in the text the differ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Solid State Physics Essential Concepts Questions!

The Hermitian adjoint of a complex m x n matrix A is the complex conjugate of its transpose, written Af = AT = AT. For example, if then Prove (a) (A+)+ = A, (b) (zA + uB)+ = z-A+ + w-B+ for z, w C,...

Show that z = r [cos() + i sin()] is the complex conjugate of z = r (cos + i sin ) Then find (a) zz and (b) z / z, z 0.

There are several steps involved in the fraud theory approach. What are they?

(a) In SystemVerilog, what is the difference between: (i) The ternary operator ? and if...then...else statements? [2 marks] (ii) always_ff and always_comb? [2 marks] (iii) Blocking, non-blocking and...

Here are definitions of sequences and trees with integer elements: type iseq = Nil | Cons of int * (unit -> iseq) type itree = Leaf of int | Branch of itree * itree (a) In an ascending sequence such...

In this question you will be asked to reflect on a project you have been involved in or observed, in which a design evolved, or could have evolved, through applying a theory of user behaviour. You...

Consider the trigonometric series a0 2 + X r=1 (ar cos rx + br sin rx) where a0, a1, a2, . . . and b1, b2, . . . are constants and suppose that f(x) is a periodic function of x with period 2. (a)...

In a Hopfield neural network configured as an associative memory, with all of its weights trained and fixed, what three possible behaviours may occur over time in configuration space as the net...

Let A, B be sets. Define: (a) the Cartesian product (A B) (b) the set of relations R between A and B (c) the identity relation A on the set A [3 marks] Suppose S, T are relations between A and B, and...

4 This assignment, based on the content of Unit 4 of the Study Guide, is worth 3% of your grade. We recommend that you hand it in after you complete Unit 4. You must show all of your work in order to...

Your client, Miller Leasing Company, is preparing a contract to lease a machine to Molinar Corporation for a period of 25 years. Miller has an investment cost of $250,000 in the machine, which has a...

Question 1 a) State the advantages of applying Karnaugh map instead of Boolean Laws to simplify a function. b) Let's say your ULAB student ID is 173014009. So, from the available distinct digits in...

Three years ago American Insulation Corporation issued 1 0 % , $ 8 7 0 , 0 0 0 , 1 0 - year bonds for $ 8 0 5 , 0 0 0 . American Insulation exercised its call privilege and retired the bonds for $ 8...

6. Realize that the test construction process is a continuous one. As a test sees expanded uses, consider that additional sources of error may be encountered. Develop future GT-based studies to...

Draw the carbocation intermediate that would be formed if each of the following substrates participated in a stepwise elimination process (E1). In each case, identify the intermediate carbocation as...

Draw the transition state for the reaction between tertbutyl chloride and sodium hydroxide.

The following two compounds are both secondary alkyl halides, but they undergo E2 reactions at different rates. The first compound reacts more rapidly than the second compound. Explain. Br Br

Frederick, Inc. reported net income totaling $63,600. Depreciation expense for the year was $30,000. Accounts receivable decreased by $1,650, inventory increased by $3,300, dividends paid totaled...

true or false the SEC has issued "safe harbor" rules to encourage forecasts by registrants, but it has had limited success

Sendelbach Corporation is a US.-based organization with operations throughout the world. One of its subsidatles is headquartered in Toronto. Although this wholly owned company operates primarily in...