Verify the characters in Table 6.3 for the irreducible representation 5 which has basis functions which are the three components of a vector in

Verify the characters in Table 6.3 for the irreducible representation Γ₅ which has basis functions which are the three components of a vector in real space along x, y, and z, by explicitly constructing a matrix representation for one operator in each class.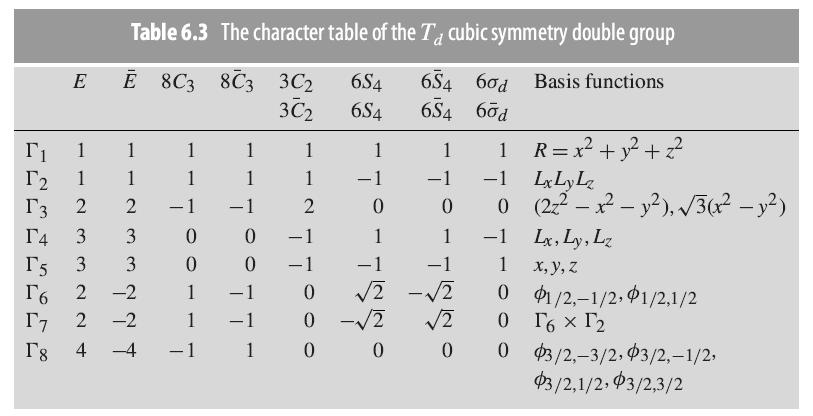

E T T 1 T3 2 Table 6.3 The character table of the Ta cubic symmetry double group 8C3 8C3 3C 654 654 60 Basis functions 302 654 6S4 60d 1 1 2 T4 3 3 T5 3 3 T6 2 -2 T7 2 -2 T8 4 T 1 1 - 1 0 0 1 1 -1 1 - 1 0 0 -1 1 1 1 2 1 0 0 0 1 -1 0 1 -1 -2 2 0 0 220 - 1 1 -1 -1 00 0 1 -1 1 0 0 16 2 0 R= x + y + z Lx LyLz (2z2-x - y), 3(x - y) Lx, Ly, Lz x, y, z 1/2,-1/2, 1/2,1/2 3/2,-3/2, 3/2,-1/2, $3/2,1/2, 3/2,3/2