Use (5.5.32) to show that in the limit of low density, the total scattering time (dephasing time)
Question:
Use (5.5.32) to show that in the limit of low density, the total scattering time (dephasing time) for an electron gas in vacuum due to Coulomb scattering at room temperature is independent of density and of the order of a femtosecond. This involves the following steps:
(a) Taking the limit kr ≫ κ, the integral in (5.5.32) becomes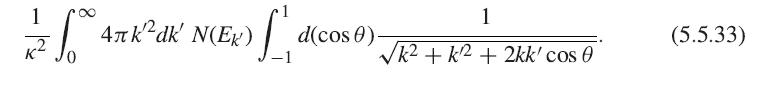
Assuming a Maxwell–Boltzmann distribution of electrons, convert the integral to a constant times a unitless integral, and perform the integral over angle and then over k′, for k determined by the condition Ek = kBT.
(b) Using the answer from part (a), calculate the rate 1/τtot using the vacuum electron mass and the permittivity of the vacuum ϵ0, and using the Debye formula (5.5.19) for κ2.
The time scale for electron–electron dephasing is typically shorter than the time scales of all other dynamic processes in solids, even at very low electron density. Time scales this short can be studied using sub-picosecond laser pulses to excite the electrons.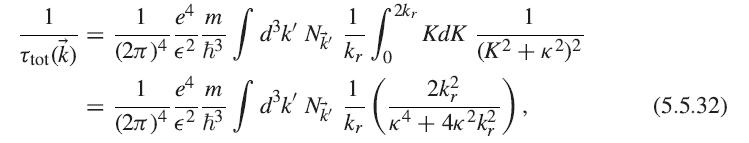

Step by Step Answer:






