An atom with spin 1 has a Hamiltonian = AS + B(2-2), where Sx, Sy, and S, are the x, y, and z components of the spin angular momentum operator. In the basis of eigenstates of the operator, S2, these three operators have the matrix representations

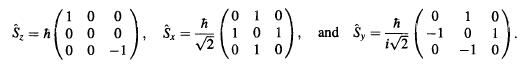
(a) Write the density matrix (in the basis of eigenstates of S) at time t = 0 for two different cases: (i) The atom is initially in an eigenstate of S, with eigenvalue +h; (ii) the atom is initially in an eigenstate of S, with eigenvalue +h.

(b) Compute the density matrix (in the basis of eigenstates of S) at timer for each of the two cases in (a).

(c) Compute the average z component of spin at timer for the two cases in (a).

Transcribed Image Text:

10 0 0 0 1 0 Sz =h00 0 0 -1 h 0 == 1 0 1 2 and Sy = -1 1 0 1 0 0 -1 0