Apply the random forest to the monthly macroeconomic data set as in Example 8.2, but using the unemployment rate as the dependent variable. You may try different choices of mtry and ntree.

Example 8.2:

To demonstrate the use of RFs, we also employ the monthly macroeconomic data used in Example 8.1. Again, the dependent variable is the monthly growth rate of US IP index and the predictors are lag-1 to lag-6 values of all available variables. Thus, we have n = 704 and k = 732. The predictors are standardized. We run the randomForest command twice to show the impact of selecting the number of predictors in each tree split. The subcommand ntree is used to specify the number of trees used and the subcommand mtry is the number of predictors used in each split. That is, g in our notation. We use the default option so that the tree is grown with the constraint that the number of data points in each leaf cannot be less than An alternative approach is to specify the maximum number of leaves a tree can have. See the subcommands nodesize and maxnodes of randomForest, respectively.

Example 8.1:

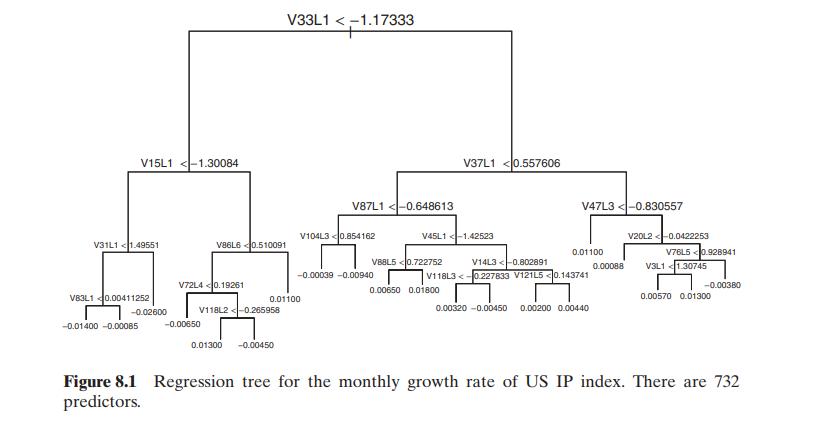
Use the industrial production (IP) growth rate as the dependent variable. The predictors consist of lag-1 to lag-6 values of all 122 variables. We standardize the predictors for ease in graphical display. The tree-based method selects a tree with 20 leaves (terminal nodes) and the residual mean deviance (i.e., squared errors) is \(2.52 \times 10^{-5}\). The 19 predictors selected for splitting are given in the \(\mathrm{R}\) demonstration below. The first split is based on lag-1 value of the 33th predictor with threshold -1.173 . The output shows that, at the root node, there are 704 observations with deviance \(3.88 \times 10^{-2}\) and sample mean 0.002163 . Also, the first leaf has five observations with deviance \(1.128 \times 10^{-4}\) and sample mean -0.01439 . Figure 8.1 displays the selected regression tree.

Transcribed Image Text:

_V15L1