EXERCISE 5.5. Consider a Brownian particle of mass m which is attached to a harmonic spring with force constant k and is constrained to move in one dimension. The Langevin equations are

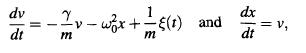
where wok/m. Let xo and vo be the initial position and velocity, respectively, of the Brownian particle and assume that it is initially in equilibrium with the fluid. Then by the equipartition theorem, the average kinetic energy is m(v) =kBT and average vibrational potential energy is w(x)=kBT. We also assume that xo and vo are statistically independent so (xovo) = 0.

(a) Show that a condition for the process to be stationary is that the noise strength is g4ykBT.

(b) Compute the velocity correlation function, ((v(12) v(t)))r

Transcribed Image Text:

dv dt 47-4x+(4) vox+ = {(1) and dx =V, dt m