Let X have the conditional geometric pmf (1)x1, x = 1, 2, . . ., where

Let X have the conditional geometric pmf θ(1−θ)x−1, x = 1, 2, . . ., where θ is a value of a random variable having a beta pdf with parameters α and β. Show that the marginal (unconditional) pmf of X is

If α = 1, we obtain

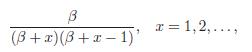
which is one form of Zipf ’s law.

Transcribed Image Text:

T(a + 3)(a + 1)(3+x-1) r(a)(3)(a +3+x) x = 1,2,....