Let X 1 ,X 2 , . . .,X n be a random sample from N(, 2 ), where both parameters and

Let X₁,X₂, . . .,X_n be a random sample from N(μ, σ²), where both parameters μ and σ² are unknown. A confidence interval for σ² can be found as follows. We know that (n − 1)S²/σ² is a random variable with a χ2(n − 1) distribution. Thus we can find constants a and b so that P((n − 1)S²/σ² 2/σ²

(a) Show that this second probability statement can be written as

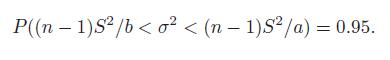
(b) If n = 9 and s² = 7.93, find a 95% confidence interval for σ².

(c) If μ is known, how would you modify the preceding procedure for finding a confidence interval for σ²?

P((n 1)S/b