Problem 10.8. A paramagnetic system sits in a constant external field, Hoz, and therefore has constant magnetization, Moz. Assume that this is the equilibrium configuration of the system and that a small uniform time-dependent magnetic field, H(t) Hicos(wpt) is applied to the system. The magnetization then becomes time- dependent. Its equation of motion can be written

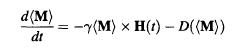
(these are called Bloch equations), where (M) = Tr(M) = Mx(1)x + My(1)+ (Mo Mz(t), H(t) = Ho2 + H(t), and D((M)) is a damping term due to interactions between particles in the medium. The constant y equals gu/h, where g is the Lande g-factor and is the magnetic moment of particles in the system.

(a) Write the equations of motion for M,(t), M,(t), and M(1), assuming Dx = Mx/T2, Dy = My/T2, and DM/T. The equations you derive will be nonlinear functions of H, Mx, My, and M.

(b) Assume that H, M., My, and M are small, so the equations can be linearized. If we define the response matrix, K(t), from the equation (M(t)) =dr'K(tr). H(r), find X(w) and Kxx(t). Write the expression for Xxx(w) in the limits 1/7 0 and 1/720.

(c) Compute the average power absorbed during the period T = 2/wo. (Note that *, , and 2 are unit vectors in the x, y, and z directions, respectively.)

Transcribed Image Text:

d(M) dt -(M) x H(1) D((M))