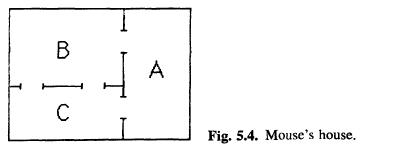
Problem 5.4. The doors of the mouse's house in Fig. 5.4 are fixed so that they periodically get larger and smaller. This causes the mouse's transition probability between rooms to become time periodic. Let the stochastic variable Y have the same meaning as in Problem 5.3. The transition matrix is now given by Q1,1(s) Q2,2(s) = Q3,3(s) = 0, Q1,2(s) cos (s/2), Q13(s) = sin(S/2), 22,1(s)=+sin(S/2), Q23(s) = + cos (S/2), Q3,1 (s) = cos (TS/2), and 23,2(s)+sin(s/2).

(a) If initially the mouse is in room A, what is the -

probability to find it in room A after 2s room changes? In room B?

(b) If initially the mouse is in room B, what is the probability to find it in room A after 2s room changes? In room B?

Transcribed Image Text:

B A C Fig. 5.4. Mouse's house.