Problem S10.10. Consider a magnetic crystal whose magnetic interactions are governed by the Hamiltonian, = {(\ -g)Sa Sp, where a and 8 denote lattice

- sites and the coupling constant, (rare), depends only on the magnitude of the displacement, ra- rs, between sites a and 3. The ith component (i = x, y, z) of the magnetization operator is M,(r) = Siad(r-ra), where ra is the position operator for the ath lattice site and Sia is the ith component of the spin operator for that site. The total spin of the lattice can be written Sitor drM(r). The total spin operator commutes with the Hamiltonian, so the spin density (the magnetization operator) satisfies the balance equation

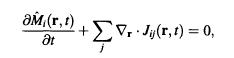
where J(r,t) is a magnetization current. Consider only long-wavelength modes so the discreteness of the lattice can be neglected. Assume that (Stor) = Mo and ($x,tot) = ($x,tot) = 0. Compute the spectral density matrix

and determine its poles to lowest nonzero order in k. Describe the hydrodynamic excitations in this system. What is unusual about them?

M,(r,t) at +Vr Jy (r,t) = 0,