The multivariant Gaussian distribution with zero mean can be written

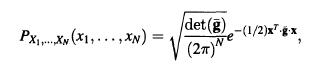
where is a symmetric N x N positive definite matrix, x is a column vector, and the transpose of x, x = (x1,...,xw), is a row vector. Thus, xgx=18xx;.

(a) Show that Pxx(x1,...,xN) is normal- ized to one.

(b) Compute the characteristic function, fx, XN (K1,..., KN).

(c) Show that the moments, (x) = 0 and that all higher moments can be expressed in terms of products of the moments, (x) and (x,x;). This is the simplest form of Wick's theorem used in field theory. ---

Transcribed Image Text:

PXX (X1,XN) det(g)-(1/2)xgx (2)Ne