6.95 Standard deviation of a discrete probability distribution The variance of a probability distribution of a random
Question:
6.95 Standard deviation of a discrete probability distribution The variance of a probability distribution of a random variable is a weighted average of its squared distances from the mean m. For discrete random variables, it equals s2 = 1x - m22P1x2.
Multiply each possible squared deviation 1x - m22 by its probability P(x) and then add. The standard deviation s is the positive square root of the variance. The table below shows the probability distribution for the number of games played in a best of seven series when each team has a 50% (taken from Example 2) or 99% chance of winning a game.
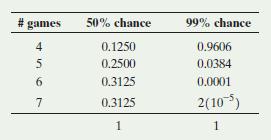
a. Find the standard deviation of X = number of games played to determine a winner when each team has a 50% chance of winning a game. (In Example 3, the mean was found to be equal to 5.8125.)
b. The table also shows the probability distribution when one team has a 99% chance of winning each game. Would you expect the standard deviation for this distribution to be smaller or larger than the one in part a? (Hint: Note how almost all the time the game will end after 4 games.)
Step by Step Answer:

Statistics The Art And Science Of Learning From Data
ISBN: 9781292164878
4th Global Edition
Authors: Alan Agresti, Christine A. Franklin, Bernhard Klingenberg






