Suppose that the average birth weights of babies born at hospitals owned by a major health maintenance organization (HMO) are approximately normal with mean 6.75 pounds and standard deviation 0.54 pound. What proportion of babies born at these hospitals weigh between 6 and 7 pounds? Find the 95th percentile of these birth weights.

1. Enter the two values for x (6 and 7) in the first two cells of column C1. Proceed as in Example 6.16, again selecting Calc ➤ Probability Distributions ➤ Normal. This time, enter the values for the mean (m 56.75) and standard deviation (s 5.54) in the appropriate boxes, and select column C1 (“x”) for the Input column. Make sure that the radio button marked “Cumulative probability” is selected and click OK. In the Session window, you will see that P(x #7)5.678305 and P(x #6)5.082433.

2. Finally, use the values calculated by MINITAB to calculate P(6, x, 7)5P(x, 7)2P(x, 6)5.6783052.0824335.595872.

3. To calculate the 95th percentile, selecting Calc ➤ Probability Distributions

➤ Normal, enter the values for the mean (m 56.75) and standard deviation (s 5.54) in the appropriate boxes, and make sure that the radio button marked “Inverse cumulative probability” is selected. We need a value x with area .95 to its left. Enter .95 in the box marked “Input constant” and click OK. In the Session window, you will see the 95th percentile, as shown in Figure 6.26.

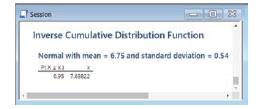
That is, 95% of all babies born at these hospitals weigh 7.63822 pounds or less. Would you consider a baby who weighs 9 pounds to be unusually large?

Transcribed Image Text:

Session Inverse Cumulative Distribution Function Normal with mean -6.75 and standard deviation = 0.54