Question: Here are two random variables that are uncorrelated but not independent. Let X and Y have the following joint probability mass function: a. Use the

Here are two random variables that are uncorrelated but not independent. Let X and Y have the following joint probability mass function:

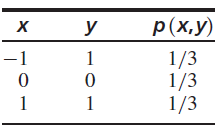
p (х,у) х y -1 1 1/3 1/3 1/3

a. Use the definition of independence on page 141 to show that X and Y are not independent (in fact
Y = |X|, so Y is actually a function of X). 

b. Show that X and Y are uncorrelated.

p (,) y -1 1 1/3 1/3 1/3

Step by Step Solution

★★★★★

3.42 Rating (168 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

a PX 1 13 PY 1 23 PX 1 and Y 1 13 6 ... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Statistics Engineers Scientists Questions!

Q:

Find an example (other than the one given in Example 5.15) of two random variables that are uncorrelated but not independent.

Q:

Suppose that X and Y are two random variables, which may be dependent, and Var(X) = Var(Y). Assuming that 0

Q:

Let D 1 and D 2 be the outcomes of two dice rolls. Let X = D 1 + D 2 be the sum of the two numbers rolled. Let Y = D 1 D 2 be their difference. Show that X and Y are uncorrelated, but not...

Q:

The elapsed time (in minutes) between the arrival of west-bound trains at the St. George subway station is an exponential random variable with a value of ? = .2. a) What are the expected value and...

Q:

Question 16 NM yet answered Marked out of 2.00 V Flag question This is a good exercise to practice calculating joint probabilities and covariance or calculating independence, to show understand of...

Q:

7. Let X1, X2, X3, X4 be a random sample of size 4 from a standard normal population. Find the sampling distribution (if possible) and moment generating function of the statistic 2X2 1 +3X2 2 +X2 3...

Q:

Th e ratio of defected switches in the production of these lines is 0.03 , 0.04, 0.01, 0.02 and 0.01 respectively, and required the following: a We draw a transistor of the total production of the...

Q:

Q1) Which two of the accompanying portray predisposition difference compromise among MC and TD? A) The MC calculation decreases fluctuation by testing until the terminal state, prompting higher...

Q:

ECSE 521A Prof. Bajcsy Assignment 2 - parts 1 & 2 Due: October 21 McGill University Fall 2015 Problems 1: Channel Capacity Theorem QuickBucks Telecom Ltd. has purchased an optical Internet link...

Q:

8. (15 points, 5+5+5) Suppose the heights of a high school students X ~ N(55, 64). Using probability Table V, (1). Find P(52 50). (3). Find P[(X - 53) (X -59) > 0]9. (10 points, 3+3+2+2) Let random...

Q:

Following are the four assertions about account balances that can be applied to the audit of a companys PP& E, including assets the company has constructed itself: existence, rights and obligations,...

Q:

Refer to the KC Toys facts in Short Exercise 5-2. Requirements 1. Journalize the following transactions. Explanations are not required. a. Purchase of the goods on July 8, 2012. b. Return of the...

Q:

Which of the following types of securities is referred to as a hytorid security? Preferied stock Cerporste bent Founder' thams foreign equaty Growth stock

Q:

3. The weekly number of luxury and compact cars sold by Honest Abe Smith at the Auto Mart, a local car dealership, can be represented as the outcome of a bivariate random variable (X,Y) with the...

Q:

Refer to Exercise 17. It is discovered that the mean of the sample used to compute the confidence bound is X = 3.40. Is it possible to determine whether P

Q:

True or false: If P = 0.02, then a. The result is statistically significant at the5%level. b. The result is statistically significant at the1%level. c. The null hypothesis is rejected at the 5%...

Q:

In each of the following situations, state the most appropriate null hypothesis regarding the population mean . a. A new type of battery will be installed in heart pacemakers if it can be shown to...

Q:

A change in expected inflation affects both the supply and demand for bonds. True/False A change in the interest rate does not shift the demand for bonds. True/False 3. An increase in the expected...

Q:

Ghost, Inc., has no debt outstanding and a total market value of $185,000. Earnings before interest and taxes, EBIT, are projected to be $29,000 if economic conditions are normal. If there is strong...

Q:

attach excel in the answer QM0.2 a) The following table shows bets for several companies. Calculate each stock's expected rate of return in CAPM. Assume the risk free rate of interestis 9 percent....