A general proof of the fact that 2 possesses approximately a chi-square sampling distribution when n

A general proof of the fact that χ 2 possesses approximately a chi-square sampling distribution when n is large is beyond the scope of this text. However, it can be justified for the binomial case (k = 2). In Optional Exercise 6.118 (p. 259), we stated that if Z is a standard normal random variable, then Z2 is a chi-square random variable with 1 degree of freedom. Denote the two cell counts for a binomial experiment as n₁ = Y and (n - Y). Then, for large n,

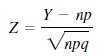
has approximately a standard normal distribution and Z² will be approximately distributed as a chi-square random variable with 1 degree of freedom. Show algebraically that for k = 2, x² = Z².

Transcribed Image Text:

Y - пр Z = V npa пра