Refer to the American Journal of Physics (June 2010) study of sound waves in a spherical cavity, Exercise 10.54. You fit a straight line model relating frequency (y) of sound waves resulting from striking a basketball with a metal rod to number of resonances (x) and determined the model was adequate for predicting y.

a. Use the least squares prediction equation to calculate the residuals for the model.

b. Plot the residuals against number of resonances (x). Do you detect a trend?

c. Based on the residual plot, which assumption appears to be violated?

d. What model modification do you recommend?

Data from Exercise 10.54

Refer to the American Journal of Physics (June 2010) study of sound waves in a spherical cavity, Exercise 10.7. You fit a straight line model relating frequency of sound waves (y) to number of resonances (x) using the data provided in Exercise 10.7.

Data from Exercise 10.7

Refer to the American Journal of Physics (June 2010) study of sound waves in a spherical cavity, Exercise 2.29. The frequencies of sound waves (estimated using a mathematical formula) resulting from the first 24 resonances (echoes) after striking a basketball with a metal rod are reproduced in the next table. Recall that the researcher expects the sound wave frequency to increase as the number of resonances increase.

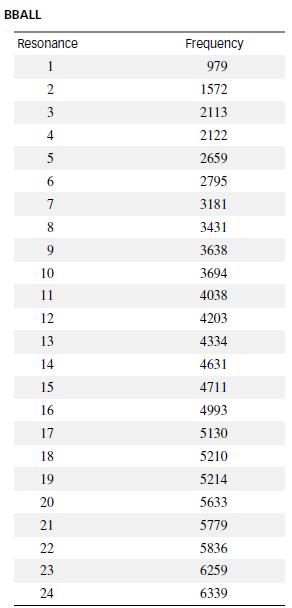
Data from Exercise 2.29

In Environmental Geology (Vol. 58, 2009) computer simulation was employed to estimate how far a block from a collapsing rock wall will bounce—called rebound length—down a soil slope. Based on the depth, location, and angle of block-soil impact marks left on the slope from an actual rock fall, the following 13 rebound lengths (meters) were estimated. Compute the mean and median of the rebound lengths and interpret these values.

Transcribed Image Text:

BBALL Resonance Frequency 1 979 2 1572 3 2113 4 2122 5 2659 6. 2795 7 3181 8. 3431 3638 10 3694 11 4038 12 4203 13 4334 14 4631 15 4711 16 4993 17 5130 18 5210 19 5214 20 5633 21 5779 22 5836 23 6259 24 6339