Since o , 1 , k are independent of s 2 , it follows that l a o o a 1 1 a k k is independent of s 2 Use this fact and Theorems 11 2 and 11 3 to show that has a Students T distribution with n (k 1) degrees of freedom e E() T sVa' (X'X)a...

The Answer is in the image, click to view ...

Since o , 1 , ... k are independent of s 2 , it

Question:

Since β̂_o, β̂₁, ... β̂_k are independent of s², it follows that

l = a_oβ̂_o + a₁β̂₁ + ...... + a_kβ̂_k

is independent of s². Use this fact and Theorems 11.2 and 11.3 to show that

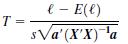has a Student’s T distribution with [n - (k + 1)] degrees of freedom.

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

Statistics For Engineering And The Sciences

ISBN: 9781498728850

6th Edition

Authors: William M. Mendenhall, Terry L. Sincich

See More Books

Question Posted: Apr 30, 2021 01:36 AM

See More Questions

Use limit theorems to show that the following functions are continuous on [0,1]. a) b) c) d) sin x cos x x +x-2 x#1 2 0 f(x) = 0
Show that if n and k are integers with 1 ¤ k ¤ n, then
Show that the F distribution with 4 and 4 degrees of freedom is given by And use this density to find the probability that for independent random samples of size n = 5 from normal populations with...
Write a function named "count the" in C which counts the number of times a given word "the" appears in the string parameter. Test Data: Input: The string where the word the present more than once....
Refer to Figure 7.1.4a, and suppose that p1 - p2 = 10 lb/in.2, A = 3 in.2, and mg = 600 lb. If the mass starts from rest at x(0) = 0, how far will it move in 0.5 sec, and how much hydraulic fluid...
Price $75.21 EPS $6 Debt $1,090M Equity $17,470M Cash $7,260M EBITDA $4,809M Shares 866M Sharp Toys Inc. manufactures children's toys. Select financial information on the company is provided in the...
A possible contributor to rising health care costs in the United States is obesity, which is currently determined using a formula called body mass index (BMI). This index is calculated using the...
Compare briefly the major types of employment interviews described in this chapter. Which type would you prefer to conduct? Why?
Selling price Expenses: Variable Fixed ( based on a capacity of 5 0 , 0 0 0 tons per year ) Net operating income $ 8 8 $ 6 0 1 8 , 7 8 $ 1 0 Hrubec Products has just acquired a small company that...
Sweet Acacia Ranch & Farm is a distributor of ranch and farm equipment. Its products include small tools, power equipment for trench-digging and fencing, grain dryers, and barn winches. Most...
Let l = y = o , + 1 x 1 + 2 x 2 , ... k x k . Use the T statistic of Exercise 11.13, in conjunction with the pivotal method, to derive the formula for a (1 - )100% confidence interval for E(y).
Zoning is defined as the distribution of vacant land to residential and nonresidential uses via policy set by local governments. Although the negative effects of zoning have been studied (e.g.,...
Develop a plan to address key stakeholder concerns from each perspective. Can you find a pathway in the stakeholder analysis to build support for your key goals?
reflective account of your development as a postgraduate learner since joining SBS considering the points below. Critically reflect on one or more points below: Assessment Criteria Use a reflective...
Technology, strategy, size, and environment are among the factors that influence leaders' choice of organization structure (Schulman, 2020). The leaders must consider the technology to be used in the...
6. Answer the following briefly. a.What is the metric and its hurdle rate for an "Enterprise" to increase its enterprise value? b.What is the metric and its hurdle rate for the corporation's equity...
Name the two major preceding management theories that contributed to the development of quality management theory. Briefly explain the major concepts of each of these preceding theories that were...
922-19x 8 After finding the partial fraction decomposition. (22 + 4)(x-4) dx = dz Notice you are NOT antidifferentiating...just give the decomposition. x+6 Integrate -dx. x33x The partial fraction...
The input to a receiver has a signal component having the PSD S S (f) = 5(f/7). The noise component is (10 -4 ) II(f/20). Determine the SNR in dB.
Global.asax is used for: a. declare application variables O b. all other answers are wrong O c. declare global variables O d. handle application events
The smooth uniform rod AB is supported by a ball-and-socket joint at A, the wall at B, and cable BC. Determine the components of reaction at A, the tension in the cable, and the normal reaction at B...
Determine the force in each member of the Pratt truss, and state if the members are in tension or compression. 2 m K. 2 m 2 m AG C E -2 m--2 m--2 m--2 m--2 m--2 m- |B 10 kN 10 kN 20 kN
Members AB and BC can each support a maximum compressive force of 800 lb, and members AD, DC, and BD can support a maximum tensile force of 1500 lb. If a = 10ft, determine the greatest load P the...
Which of the following journal entries will record the payment of a $1,500 salaries payable originally incurred for Salaries Expense? Select one: A. Debit Salaries Expense; credit Salaries Payable B....
What is the definition of substantially appreciated inventory? A. Inventory with a FMV greater than its basis B. Inventory and unrealized receivables with a FMV greater than their basis C. Inventory...
Case Products manufactures two models of DVD storage cases: regular and deluxe. Presented is standard cost information for each model: Cost Components Regular Deluxe Direct materials Lumber 2 board...

Since o , 1 , ... k are independent of s 2 , it

Question:

e - E(€) T = sVa' (X'X)a

Step by Step Answer:

Statistics For Engineering And The Sciences

Students also viewed these Engineering questions