Sintering, one of the most important techniques of materials science, is used to convert a powdered material

Question:

Sintering, one of the most important techniques of materials science, is used to convert a powdered material into a porous solid body. The following two measures characterize the final product:

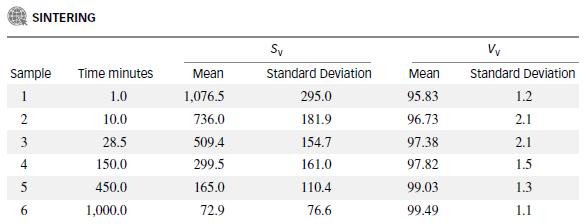
When V_v = 100%, the product is completely solid—i.e., it contains no pores. Both V_v and S_v are estimated by a microscopic examination of polished cross sections of sintered material. Generally, the longer a powdered material is sintered, the more solid will be the product. Thus, we would expect S_v to decrease and V_v to increase as the sintering time is increased. The table at the bottom of the page gives the mean and standard deviation of the values of S_v (in squared centimeters per cubic centimeter) and V_v (percentage) for 100 specimens of sintered nickel for six different sintering times.*

a. Plot the sample means of the S_v measurements versus sintering time. Hypothesize a linear model relating mean S_v to sintering time x.

b. Plot the sample means of the V_v measurements versus sintering time. Hypothesize a linear model relating mean V_v to sintering time x.

c. Fit a linear model relating E(S_v) to sintering time x. Show that the data may violate the assumptions of Section 11.2. What model modifications do you suggest?

d. Consider second-order model relating V_v to sintering time x. Fit the model E(V_v) = β_o + β₁x + β₂x² to the data and conduct a complete regression analysis. Ultimately, you want to predict the value of V_v at sintering time 150 minutes.

e. The unstable values of the standard deviations for S_v shown in the table indicate a strong possibility that the standard regression assumption of equal variance is violated for the model of part c. We can satisfy this assumption by transforming the response to a new response that has a constant variance. Consider the natural log transform^* S_v^* = ln(S_v). Fit the model E (S_v^*) = β_o + β₁x to the data and give the leastsquares
prediction equation.

f. Is the model in part e adequate for predicting ln(S_v)? Test using α = .05.

g. Refer to the model, part e. The predicted value of S_v is the antilog,

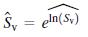
To obtain a prediction interval for S_v, you need to take the anti logs of the endpoints of the prediction interval for S_v^*.^† Find a 95% prediction interval for S_v when the sintering time is 150 minutes.