Let \

(a,

b, c, d\) be any numbers with \(a

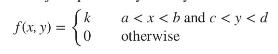
In other words, \(f(x, y)\) is constant on the rectangle \(a

a. Show that \(k=\frac{1}{(b-a)(d-c)}\).

b. Show that the marginal density of \(X\) is \(f_{X}(x)=\) \(1 /(b-a)\) for \(a

c. Show that the marginal density of \(Y\) is \(f_{Y}(y)=\) \(1 /(d-c)\) for \(c

d. Use parts (a), (b), and

(c) to show that \(X\) and \(Y\) are independent.

Transcribed Image Text:

f(x, y) = (k to a