Using the data from Table 2, construct a (95 %) confidence interval estimate of the mean difference,
Question:
Using the data from Table 2, construct a \(95 \%\) confidence interval estimate of the mean difference, \(\mu_{d}\).
By Hand Approach
Step 1 Compute the differenced data. Because the sample size is small, we must verify that the differenced data come from a population that is approximately normal with no outliers.
Step 2 Compute the sample mean difference, \(\bar{d}\), and the sample standard deviation difference, \(s_{d}\).
Step 3 Determine the critical value, \(t_{\frac{\alpha}{2}}\), with \(\alpha=0.05\) and \(n-1\) degrees of freedom.
Step 4 Use Formula (1) to determine the lower and upper bounds.
Step 5 Interpret the results.
Technology Approach
Step 1 Compute the differenced data. Because the sample size is small, verify the differenced data come from a population that is approximately normal with no outliers.
Step 2 Use a statistical spreadsheet or graphing calculator with advanced statistical features to obtain the confidence interval. We will use a TI-84 Plus \(\mathrm{C}\) to construct the confidence interval. The steps for constructing confidence intervals using StatCrunch, Minitab, Excel, and the TI-83/84 graphing calculators are given in the Technology Step-by-Step.
Step 3 Interpret the result.
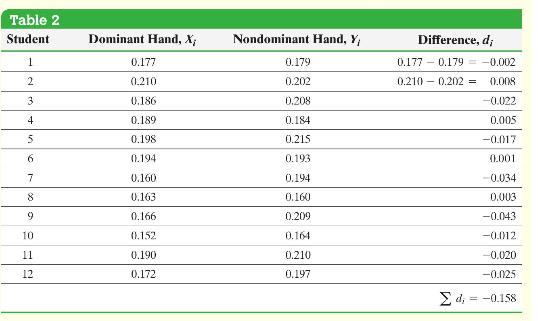
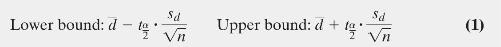
Step by Step Answer:

Statistics Informed Decisions Using Data
ISBN: 9781292157115
5th Global Edition
Authors: Michael Sullivan





