One hundred one-acre test plots are being used to assess the yield potential of a new variety of wheat genetically engineered by Washington State University. The actual yield-per-acre observations on the test plots can be viewed as iid observations from some log-normal population, so that the statistical model for the experiment is given by

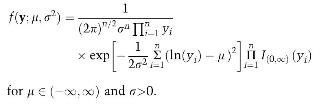
a. Define minimal sufficient statistics for \(f\left(\mathbf{y} ; \mu, \sigma^{2}ight)\).

b. Are the sufficient statistics you defined in

(a) complete sufficient statistics?

c. Is \(t_{1}(\mathbf{Y})=n^{-1} \sum_{i=1}^{n} \ln \left(Y_{i}ight)\) the MVUE of the parameter \(\mu\) ? Is it consistent? Why?

d. Is \(t_{2}(\mathbf{Y})=(n-1)^{-1} \sum_{i=1}^{n}\left(\ln \left(Y_{i}ight)-n^{-1} \sum_{i=1}^{n} \ln \left(Y_{i}ight)ight)^{2}\) the MVUE of the parameter \(\sigma^{2}\) ? Is it consistent?

e. Define a consistent estimator of \(q(\mu, \sigma)=e^{\mu+\sigma^{2} / 2}\), which is the mean of the log-normal population. Justify your answer. (The MVUE of the mean exists, but it is quite complicated to define and calculate. See D. J. Finney (1941), "On the distribution of a variate whose logarithm is normally distributed." Roy. Statistical Society, Series B, 7, pp. 155-161.)

f. An overworked, underpaid, gaunt-looking research assistant hands you an envelope that contains only summary information on the results of the experiment. In particular the information is that

\(\sum_{i=1}^{100} \ln \left(Y_{i}ight)=375.00, \sum_{i=1}^{100}\left(\ln \left(Y_{i}ight)ight)^{2}=1455.75\).

Generate an estimate of \(q\left(\mu, \sigma^{2}ight)_{(2 \times 1)}=\left[\begin{array}{c}\mu \\ \sigma^{2}\end{array}ight]\) using the MVUE of \(q\left(\mu, \sigma^{2}ight)\). Generate an estimate of the mean of the lognormal distribution using a consistent estimator.

Transcribed Image Text:

f(y: 1,)= 1 (2) x exp[- for (x,x) and a>0. IY 1 277 2 (In(1) 14 )] (0.0) (x2)