Exercises B.24 and B.25 describe a study to determine whether a sales tax on soda will reduce consumption of soda in the US below the current per-capita level of about 50 gallons of soda per year. The hypotheses for the test are H₀: μ = 50 vs H_a: μ < 50, where μ represents the average annual consumption of soda in communities where the sales tax is implemented.

(a) Suppose sample results give a p-value of 0.02. Interpret this p-value in terms of random chance and in the context of taxes and soda consumption.

(b) Now suppose sample results give a p-value of 0.41. Interpret this p-value in terms of random chance and in the context of taxes and soda consumption.

(c) Which p-value, 0.02 or 0.41, gives stronger evidence that a sales tax will reduce soda consumption?

(d) Which p-value, 0.02 or 0.41, is more statistically significant?

Exercise B.25

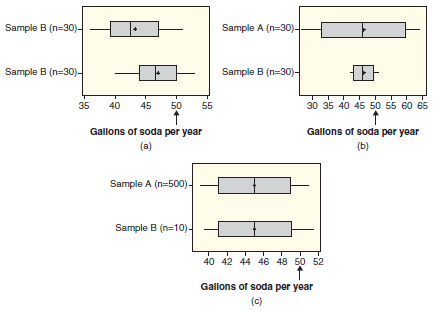
We extend the situation described in Exercise B.24 to each of the pairs of boxplots in Figure B.9. In each case, indicate whether the results of Sample A or Sample B show stronger evidence that average consumption of taxed soda is below 50, or state that neither sample shows evidence of this. Notice that sample sizes are shown on the side of the boxplots.

Figure B.9

Exercise B.24

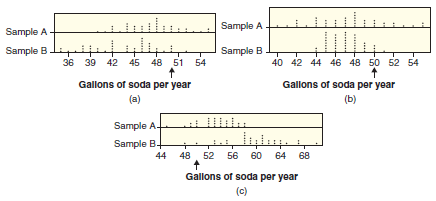
The average American drinks approximately 50 gallons of soda (pop) a year, delivering approximately 50,000 calories and no nutrition. Some legislators are recommending instituting a sales tax on soda to raise revenue and fight obesity. Will a sales tax impact consumption? Suppose that a sales tax on soda will be added in a random sample of communities to measure the impact on soda consumption. We wish to determine whether average per-capita consumption of taxed soda is significantly less than 50 gallons a year. Figure B.8 shows dotplots of three pairs of possible sample results. In each case, indicate whether the results of Sample A or Sample B show stronger evidence that average consumption of taxed soda is below 50, or state that neither sample shows evidence that the mean is below 50. Explain your reasoning in each case.

Figure B.8

Transcribed Image Text:

Sample B (n=30)- Sample A (n=30)- Sample B (n=30)- Sample B (n=30)- 35 40 45 50 55 30 35 40 45 50 55 60 65 Gallons of soda per year Gallons of soda per year (a) (b) Sample A (n=500) - Sample B (n=10)- 40 42 44 46 48 50 52 Gallons of soda per year (c) Sample A Sample A- Sample Bli Sample B 36 39 42 45 48 51 54 40 42 44 46 48 50 52 54 Gallons of soda per year Gallons of soda per year (a) (b) Sample A Sample B- 44 48, 52 56 60 64 68 Gallons of soda per year (c) ......