In Data 4.6 we look at finger-tapping rates to see if ingesting caffeine increases average tap rate. The sample data for the 20 subjects (10 randomly getting caffeine and 10 with no-caffeine) are given in Table 4.4 on page 241. To create a randomization distribution for this test, we assume the null hypothesis μ_c= μ_nis true, that is, there is no difference in average tap rate between the caffeine and no-caffeine groups.

Table 4.4

(a) Create one randomization sample by randomly separating the 20 data values into two groups. (One way to do this is to write the 20 tap rate values on index cards, shuffle, and deal them into two groups of 10.)

(b) Find the sample mean of each group and calculate the difference, xÌ…_c ˆ’ xÌ…_n, in the simulated sample means.

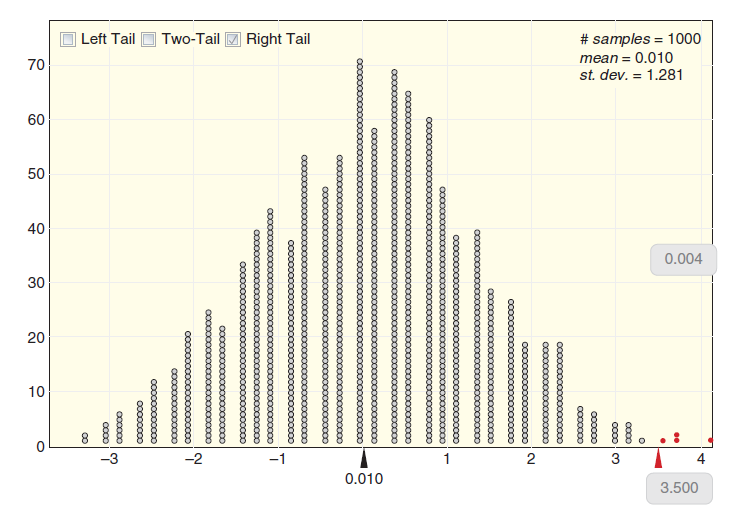
(c) The difference in sample means found in part (b) is one data point in a randomization distribution. Make a rough sketch of the randomization distribution shown in Figure 4.11 on page 242 and locate your randomization statistic on the sketch.  

Data 4.6

Many people feel they need a cup of coffee or other source of caffeine to €˜€˜get going€ in the morning. The effects of caffeine on the body have been extensively studied. In one experiment,14 researchers trained a sample of male college students to tap their fingers at a rapid rate. The sample was then divided at random into two groups of 10 students each. Each student drank the equivalent of about two cups of coffee, which included about 200 mg of caffeine for the students in one group but was decaffeinated coffee for the second group. After a 2-hour period, each student was tested to measure finger tapping rate (taps per minute). The students did not know whether or not their drinks included caffeine and the person measuring the tap rates was also unaware of the groups. This was a double-blind experiment with only the statistician analyzing the data having information linking the group membership to the observed tap rates. (Think back to Chapter 1: Why is this important?) The goal of the experiment was to determine whether caffeine produces an increase in the average tap rate. The finger-tapping rates measured in this experiment are summarized in Table 4.4 and stored in CaffeineTaps.

Figure 4.11

Transcribed Image Text:

Caffeine 248 250 246 245 248 245 250 Mean = 248.3 Mean = 244.8 252 248 248 247 250 246 246 242 248 242 No caffeine 242 244 244 O Left Tail Two-Tail M Right Tail # samples = 1000 mean = 0.010 70 st. dev. = 1.281 60 50 40 0.004 30 10 -2 -1 1 4. 0.010 3.500 C00000 Co00000 2. coo 00000000 20