The following table lists the minimum percent of data in any distribution and the actual percent of data in the normal distribution between ± 1.1, ± 1.5, ± 2.0, and ± 2.5 standard deviations from the mean. The minimum percents of data in any distribution were calculated by using Chebyshev’s theorem. The actual percents of data for the normal distribution were calculated by using the area given in the standard normal, or z, table.

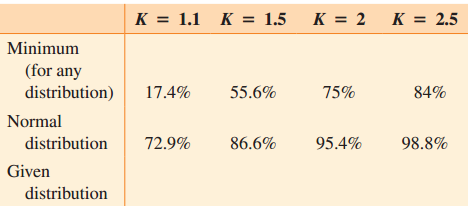
The third row of the chart has been left blank for you to fill in the percents when you reach part (e). 

Consider the following 30 pieces of data obtained from a quiz. 

1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 4, 4, 4, 5, 6,

6, 6, 7, 7, 7, 7, 8, 8, 8, 8, 9, 9, 9, 10, 10

(a) Determine the mean of the set of scores. 

(b) Determine the standard deviation of the set of scores.

(c) Determine the values that correspond to 1.1, 1.5, 2, and 2.5 standard deviations above the mean. Then deter-mine the values that correspond to 1.1, 1.5, 2, and 2.5 standard deviations below the mean.

By observing the 30 pieces of data, determine the actual percent of quiz scores between

± 1.1 standard deviations from the mean.

± 1.5 standard deviations from the mean.

± 2 standard deviations from the mean.

± 2.5 standard deviations from the mean.

(e) Place the percents found in part (d) in the third row of the chart. 

(f) Compare the percents in the third row of the chart with the minimum percents in the first row and the normal percents in the second row, and then make a judgment as to whether this set of 30 scores is approximately normally distributed.

Transcribed Image Text:

K = 1.1 K = 1.5 K = 2 K = 2.5 Minimum (for any distribution) 75% 17.4% 55.6% 84% Normal 95.4% distribution 72.9% 86.6% 98.8% Given distribution