If the sea power plant described in Problem 11.5 is to deliver power at ($ 8 /

Question:

If the sea power plant described in Problem 11.5 is to deliver power at $\$ 8 / 10^{6} \mathrm{Btu}$, estimate the maximum permissible cost of the condenser and evaporator heat-exchanger surface in dollars per square foot, assuming a 20 -year life, $10 \%$ discount rate, and $7 \%$ yearly fuel inflation.

Problem 11.5

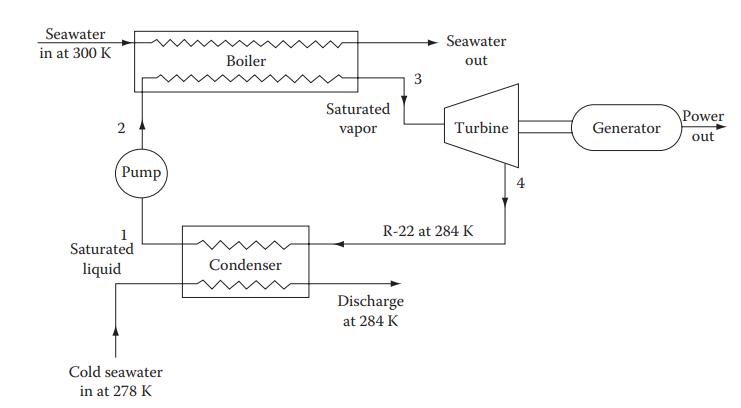
A $100 \mathrm{MW}$ ocean thermal gradient power plant is to be designed for a location where the ocean surface temperature is $300 \mathrm{~K}\left(80^{\circ} \mathrm{F}\right)$ and water at a lower depth is available at $278 \mathrm{~K}\left(40^{\circ} \mathrm{F}\right)$. If the heat exchangers are sized to operate a power plant using R-22 as the working fluid between 294 and $284 \mathrm{~K}\left(70^{\circ} \mathrm{F}\right.$ and $\left.50^{\circ} \mathrm{F}\right)$, calculate the flow rates of $\mathrm{R}-22$ and water required, assuming that the condenser heat exchangers have an overall conductance of $1000 \mathrm{~W} / \mathrm{m}^{2} \cdot \mathrm{K}\left(176 \mathrm{Btu} / \mathrm{h} \cdot \mathrm{ft}^{2}{ }^{\circ} \mathrm{F}\right)$ and an effectiveness of $100 \%$. Also calculate the plant efficiency and the surface area of the condenser. The saturation pressure of R-22 at $294 \mathrm{~K}$ is $9.38 \times 105 \mathrm{~N} \cdot \mathrm{m}^{2}$ ( $136.1 \mathrm{psia}$ ), the enthalpy is $256.8 \mathrm{~kJ} / \mathrm{kg}$ ( 110.4 $\left.\mathrm{Btu} / \mathrm{lb}_{\mathrm{m}}\right)$, and the entropy is $0.900 \mathrm{~kJ} / \mathrm{kg} \cdot \mathrm{K}\left(0.215 \mathrm{Btu} / \mathrm{lb}_{\mathrm{m}}{ }^{\circ} \mathrm{R}\right)$. The enthalpy of the saturated liquid at $284 \mathrm{~K}$ is $56.45 \mathrm{~kJ} / \mathrm{kg}$ (24.27 Btu/lb) and the heat of vaporization is 197.0 $\mathrm{kJ} / \mathrm{kg}\left(85.68 \mathrm{Btu} / \mathrm{lb}_{\mathrm{m}}\right)$. The saturation pressure at $284 \mathrm{~K}$ is $6.81 \times 105 \mathrm{~N} \cdot \mathrm{m}^{2}(98.73 \mathrm{psia})$, while the entropy at $284 \mathrm{~K}$ of the saturated liquid is $0.217 \mathrm{~kJ} / \mathrm{kg} \mathrm{K}\left(0.0519 \mathrm{Btu} / \mathrm{lb}_{\mathrm{m}}{ }^{\circ} \mathrm{R}\right)$.

Assume efficiencies for the pump and the turbine are $80 \%$ and $90 \%$, respectively. The specific volume of the saturated R-22 liquid at $284 \mathrm{~K}$ is $0.000799 \mathrm{~m}^{3} / \mathrm{kg}\left(0.0128 \mathrm{ft}^{3} / \mathrm{lb}\right)$. A schematic diagram of the system is shown as follows:

image text in transcribed