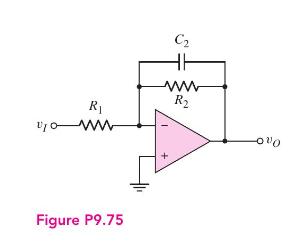
(a) Using the results of Problem 9.75, design the low-pass active filter in Figure P9.75 such that the input resistance is \(20 \mathrm{k} \Omega\), the low-frequency gain is -15 , and the \(-3 \mathrm{~dB}\) frequency is \(5 \mathrm{kHz}\).

(b) Repeat part (a) such that the input resistance is \(15 \mathrm{k} \Omega\), the low-frequency gain is -25 , and the \(-3 \mathrm{~dB}\) frequency is \(15 \mathrm{kHz}\).

Data From Problem 9.75:-

The circuit in Figure P9.75 is a first-order low-pass active filter.

(a) Show that the voltage transfer function is given by \[A_{v}=\frac{-R_{2}}{R_{1}} \cdot \frac{1}{1+j \omega R_{2} C_{2}}\]

(b) What is the voltage gain at dc \((\omega=0)\) ?

(c) At what frequency is the magnitude of the voltage gain a factor of \(\sqrt{2}\) less that the dc value? (This is the \(-3 \mathrm{~dB}\) frequency.)

Transcribed Image Text:

R Figure P9.75 C ww R