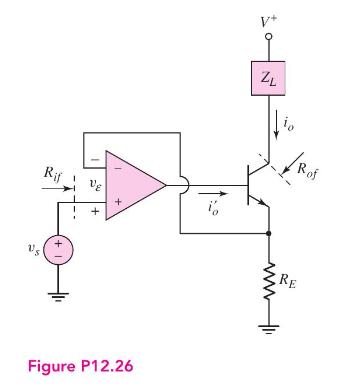
Consider the circuit in Figure P12.26. The input resistance of the op-amp is \(R_{i}=\infty\) and the output resistance is \(R_{o}=0\). The op-amp has a finite gain, so that \(i_{o}^{\prime}=A_{g} v_{\varepsilon}\). The current gain of the transistor is \(h_{F E}\).

(a) Write the closed-loop transfer function in the form

\[A_{g f}=\frac{i_{o}}{v_{s}}=\frac{A_{g}}{\left(1+\beta_{z} A_{g}\right)}\]

where \(A_{g}\) is the open-loop gain of the system.

(b) What is the expression for \(\beta_{z}\) ?

(c) If \(A_{g}=5 \times 10^{5} \mathrm{mS}\) and \(A_{g f}=10 \mathrm{mS}\), what is the required \(\beta_{z}\) and \(R_{E}\) ?

(d) If \(A_{g}\) increases by 10 percent, what is the corresponding percent change in \(A_{g f}\) ?

Transcribed Image Text:

Rif VE + Figure P12.26 V+ ZL Rof RE