Let us assume that the refractive index of the medium above the ((x), y) plane is 1
Question:
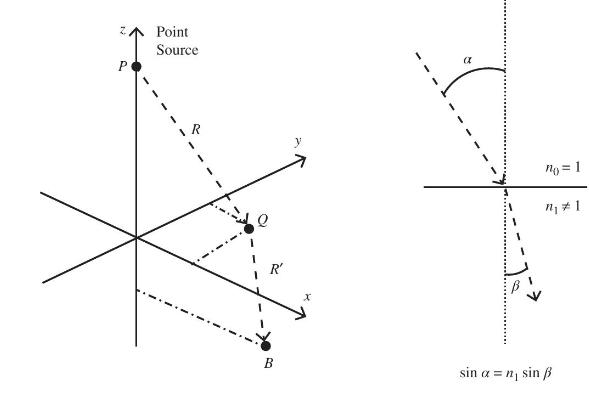
Let us assume that the refractive index of the medium above the \((x\), y) plane is 1 and that the refractive index of the medium below the \((x\), \(y\) ) plane is \(n_{1} eq 1\). Also, let us assume a point source at \((0,0, h)\) on the positive \(z\)-axis define the point \(Q\) to be an arbitrary point \((x, y, 0)\) on the boundary between the two media and the point \(B\) to be the receiver location \((a, 0, h)\). The distance from point \(P\) to point \(Q\) is \(R\) and the distance from point \(Q\) to point \(B\), is \(R^{\prime}\). See the following left figure for this situation, which is not drawn to scale. The change in entry angle from the upper medium to the bottom medium is shown in the lower right-hand image, that is, Snell's Law.
According to Huygens, the spherical wave from \(P\) is \(\frac{e^{i k R}}{R}\) at \(z=0\) for any \((x, y)\) in that plane. From \(Q\), a secondary spherical wave emerges with a beginning amplitude and a field amplitude at \(B\).
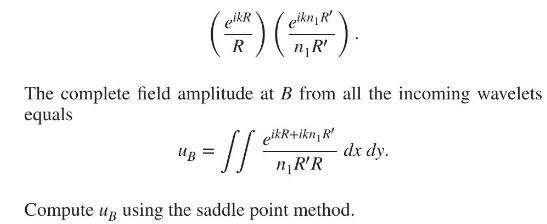
Step by Step Answer:

Free Space Optical Systems Engineering Design And Analysis
ISBN: 9781119279020
1st Edition
Authors: Larry B. Stotts





