Refer to the introduction to Problem 2.8. Assume the incident light is monochromatic with a wavelength \(\lambda=500 \mathrm{~nm}\) and slit separation. Suppose \(d=0.100 \mathrm{~mm}\). The Young's experimental geometry is shown in the following figure: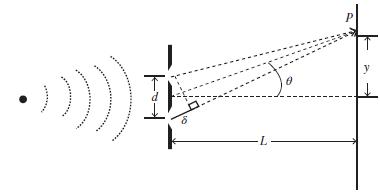

Assume \(L=1 \mathrm{~m}\).

(a) What is the phase difference \(\varphi\) between the two waves arriving at a point \(P\) on the screen when \(\theta=0.80^{\circ}\) ?

(b) What is the phase difference between the two waves arriving at a point \(P\) on the screen when \(y=4.00 \mathrm{~mm}\) ?

(c) If \(\varphi=\frac{1}{3} \mathrm{rad}\), what is the value of \(\theta\) ?

(d) If the path difference is \(\frac{\lambda}{4}\), what is the value of \(\theta\) ?

Problem 2.8

In Young's double-slit experiment, light intensity is a maximum when the two waves interfere constructively. This occurs when

where \(d\) is the separations of the slits, \(\lambda\) the wavelength of light, \(m\) the order of the maximum, and \(\theta\) the scatter angle that the maxima occurs. Assume \(d=0.320 \mathrm{~mm}\). If a beam of \(\lambda=500 \mathrm{~nm}\) light strikes the two slits, how many maxima will there be in the angular range \(45^{\circ} \leq \theta \leq 45^{\circ}\) ?

Transcribed Image Text:

T L P y