9.5 The cost of an electrostatic sensing system can be reduced by removing the charge sensor (ESV) and associated level 1 control loop. It is now required to design a three-input three-output developability control loop using three process actuators, the grid voltage, Ug(k)¼Vg(k), the exposure intensity, Ul(k)¼X(k), and the development bias, Ub(k)¼Vbias(k), and measurements from the DMA sensor. Let Dl(k), Dm(k), and Dh(k) represent the three different DMA measurements shown in the state vector, x(k), measured every pitch, indicated by the parameter, k. The linear state variable description of the control system is characterized by the Jacobian matrix at the nominal operating point {Ugo¼600 V, Ulo¼4 ergs=cm2, Ubo¼200 V}

as shown below:

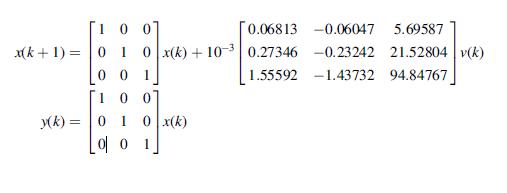
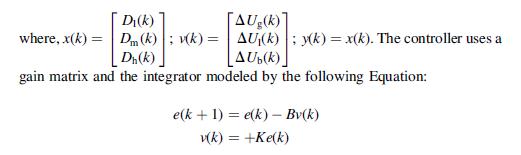
where e(k)¼xdx(k) and xd is the desired state vector.

a. Find the gain matrix for placing the poles at location [0.2, 0.2, 0.2] using Equation 9.45.

b. Show the time evolution of the states for a step response with respect to pitch number using recursive solution of Equation 4.118, the measurement-actuation updates are executed at every pitch.

c. Compare the results of step b by running the control simulation with the charge, development models from Chapter 10.

d. Are there other reasons why this type of control approaches are more suitable than level 1 and 2 architecture? Comment.

Transcribed Image Text:

100 x(k+1)= 0 0 0 1 1 0 07 y(k) = [0.06813 -0.06047 5.69587 0x(k)+103 0.27346 -0.23242 21.52804 v(k) 1.55592 -1.43732 94.84767 0 1 0x(k) 00 1