A definition for the instantaneous frequency was given in Eq. (2.49). A more general definition is (f_{i}(t)=frac{1}{2
Question:
A definition for the instantaneous frequency was given in Eq. (2.49). A more general definition is \(f_{i}(t)=\frac{1}{2 \pi} \operatorname{Im}\left\{\frac{d}{d t} \ln \psi(t)ight\}\) where \(\operatorname{Im}\) \{.\}, indicates imaginary part and \(\psi(t)\) is the analytic signal. Using this definition, calculate the instantaneous frequency for
\[
x(t)=\operatorname{Rect}\left(\frac{t}{\tau}ight) \cos \left(2 \pi f_{0} t+\frac{B}{2 \tau} t^{2}ight)
\]
Equation (2.49)
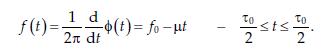
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Radar Systems Analysis And Design Using MATLAB
ISBN: 9780367507930
4th Edition
Authors: Bassem R. Mahafza
Question Posted:





