A linearly varying pressure \(p\) is applied along the edge of the 4 -node element shown in the figure. The finite element method converts the distributed force into an equivalent set of nodal forces \(\left\{\mathbf{F}^{e}\right\}\) such that

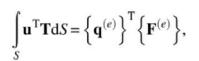where \(\mathbf{T}\) is the applied traction (force per unit area), and \(\mathbf{u}\) is the vector of displacements. Since the applied pressure is normal to the surface (in the \(x\) direction), the traction can be expressed as \(\mathbf{T}=\{p, 0\}^{T}\), where \(p\) can be expressed as \(p=p_{0}(t+1) / 2\), where \(t=-1\) at node 1 and \(t=+1\) at node 4 . The length of the edge is \(L\). Integrate the lefthand side of the above equation to compute the work-equivalent nodal forces \(\left\{\mathbf{F}^{(e)}\right\}\) when \(\left\{\mathbf{q}^{(e)}\right\}^{\mathrm{T}}=\left\{u_{1}, v_{1}, u_{2}, v_{2}\right.\), \(\left.u_{3}, v_{3}, u_{4}, v_{4}\right\}\).

Transcribed Image Text:

JuTTds={q}"{F}. S