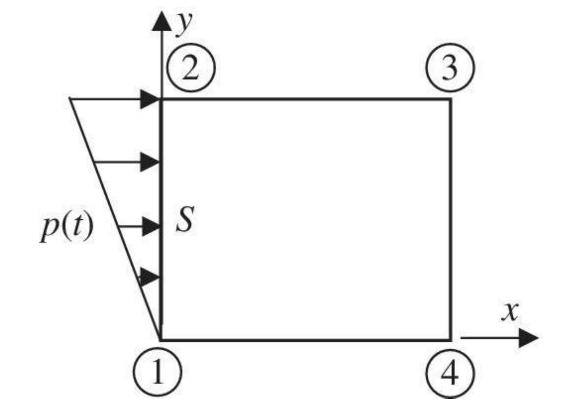
For the 4node element shown in the figure, a linearly varying pressure \(p\) is applied along the edge. The finite element method converts the distributed force into an equivalent set of nodal forces \(\left\{\mathbf{F}_{e}ight\}\) such that

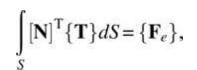
where \(\{\mathbf{T}\}\) is the traction (force per unit area) on the surface \(S\) and \([\mathrm{N}]\) is a \(2 \times 8\) matrix of shape functions. The applied pressure in the above figure is normal to the surface (in the \(x\) direction), therefore the traction can be expressed as \(\{\mathbf{T}\}=\left\{\begin{array}{ll}p & 0\end{array}ight\}^{\mathrm{T}}\) where \(p\) can be expressed as \(p=p_{0} y / L_{e} L_{e}\) is the length of the edge. Integrate the lefthand side of the equation above to compute the workequivalent nodal forces \(\left\{\mathbf{F}_{e}ight\}(8 \times 1\) vector).

S [[N]{T}dS= {Fe},