A patch test is often used to ensure that the solutions from the finite element method converge to the exact solution as the finite element mesh is refined. In the generalized form of the patch test, the patch of elements is supported by a minimum number of boundary conditions to prevent rigid body motion. For the remainder of the boundary nodes, a set of load consistent with constant stress state in the element is applied. The computed stress state should obviously match with the assumed stress state. Let a structure be approximated by four plane stress finite elements with thickness \(=0.1\), as shown in the figure with \(E=\) 1000 and \(v=0.3\).

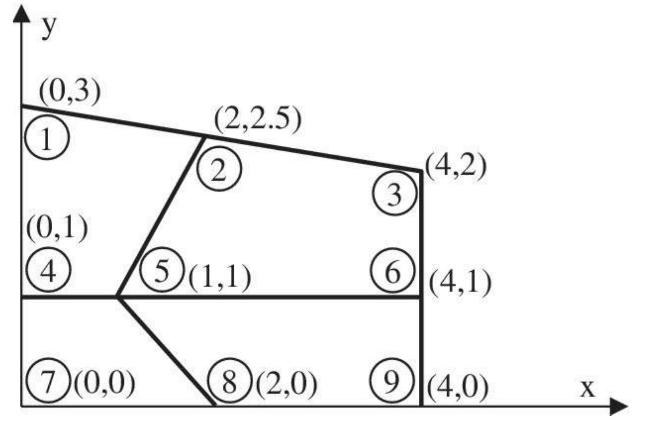
a. For all boundary nodes \((1,2,3,4,6,7,8,9)\) apply displacement boundary conditions of \(u=0.2 x\) and \(v=-0.06 y\). Using a commercial FE software, check the analysis results with the analytical solution of a constant stress field: \(\sigma_{x x}=200, \sigma_{y y}=0\), and \(\tau_{x y}=0\). You need to make sure that incompatible shape functions are removed in the analysis. Provide a discussion of patch test results.

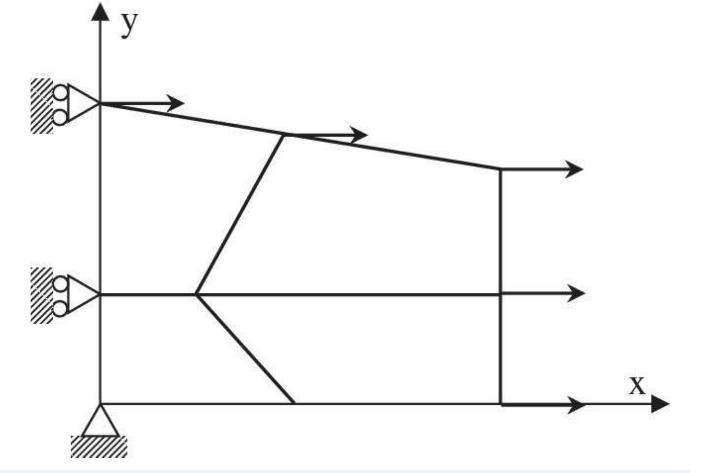
b. Instead of applying a displacement boundary condition, apply distributed traction forces that represent a constant stress field \(\sigma_{x x}=200\). Convert the distributed traction forces into work-equivalent nodal forces. In the figure shown below, draw your nodal force vectors showing their directions and magnitudes. Carry out FE analysis with these nodal forces and verify whether all elements have the constant stress field.

Transcribed Image Text:

y (0,3) (1) (2,2.5) (2) (4,2) 3. (0,1) 4 (1,1) (6 (4,1) (0,0) 8(2,0) 9(4,0) X