Consider the tapered bar in problem 17. Use the RayleighRitz method to solve the same problem. Assume the displacement in the form of \(u(x)=a_{0}+a_{1} x+a_{2} x^{2}\). Compare the solutions for \(u(x)\) and \(P(x)\) with the exact solution given below by plotting them.

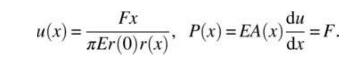
Data From Probelm 17:

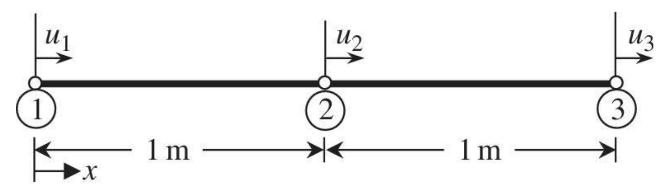
Consider a finite element with three nodes, as shown in the figure. When the solution is approximated using \(u(x)=N_{1}(x) u_{1}+N_{2}(x) u_{2}+N_{3}(x) u_{3}\), calculate the interpolation functions \(N_{1}(x), N_{2}(x)\), and \(N_{3}(x)\). Hint: Start with an assumed solution in the following form: \(u(x)=c_{0}+c_{1} x+c_{2} x^{2}\).

Transcribed Image Text:

Fx du u(x)=. Er(0)r(x)' P(x)=EA(x)=F. dr