Consider the tapered bar in problem 21. Use the RayleighRitz method to solve the same problem. Assume the displacement in the form of \(u(x)=(x-1)\left(c_{1} x+c_{2} x^{2}ight)\).

Data From Problem 21:

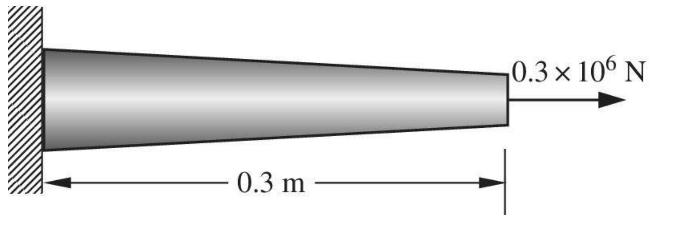
A tapered bar with circular cross section is fixed at \(x=0\), and an axial force of \(0.3 \times 10^{6} \mathrm{~N}\) is applied at the other end. The length of the bar \((L)\) is \(0.3 \mathrm{~m}\), and the radius varies as \(r(x)=0.03-0.07 x\), where \(r\) and \(x\) are in meters. Use three equallength finite elements to determine the displacements, axial force resultants, and support reactions. Compare your FE solutions with the exact solution by plotting \(u\) vs. \(x\), and \(P\) (element force) vs. \(x\). Use \(E\) \(=10^{10} \mathrm{~Pa}\).

Transcribed Image Text:

0.3 m 0.3 106 N