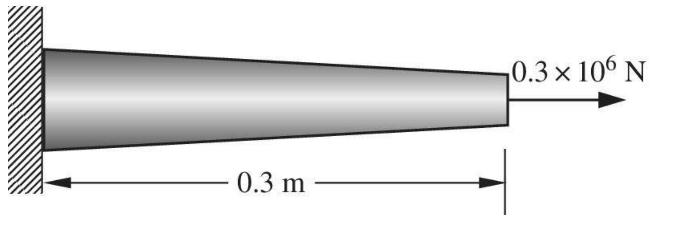
A tapered bar with circular cross section is fixed at \(x=0\), and an axial force of \(0.3 \times 10^{6} \mathrm{~N}\) is applied at the other end. The length of the bar \((L)\) is \(0.3 \mathrm{~m}\), and the radius varies as \(r(x)=0.03-0.07 x\), where \(r\) and \(x\) are in meters. Use three equallength finite elements to determine the displacements, axial force resultants, and support reactions. Compare your FE solutions with the exact solution by plotting \(u\) vs. \(x\), and \(P\) (element force) vs. \(x\). Use \(E\) \(=10^{10} \mathrm{~Pa}\).

0.3 m 0.3 106 N