For the system described by the state-space equation determine its Resolvent Matrix and the State-Transition Matrix using

Question:

For the system described by the state-space equation

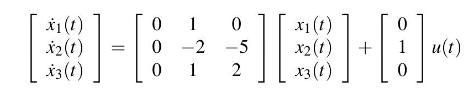
image text in transcribed

determine its Resolvent Matrix and the State-Transition Matrix using the Laplace transform. If the initial state is

\[
x_{1}(0)=2, \quad x_{2}(0)=0, \quad x_{3}(0)=2
\]
determine the time response of the states to a step function \(u(t)=2\), and if the output equation is
\[
y(t)=\left[\begin{array}{lll}
1 & 1 & 0
\end{array}ight]\left[\begin{array}{l}
x_{1}(t) \\
x_{2}(t) \\
x_{3}(t)
\end{array}ight]
\]
determine the output \(y(t)\) under these conditions.