In the following mechanical system the input is a force \(f(t)\) and the output is the spring force in \(k_{2}\).

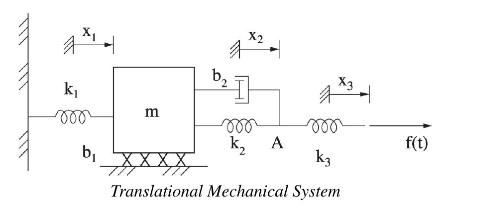
(a) Draw the free-body diagrams for the mass \(m\) and the massless point \(A\).

(b) Write down the equations of motion.

(c) Choose the minimum number of state variables for the system and develop the state-variable matrix model (i.e. obtain \(\boldsymbol{A}, \boldsymbol{B}, \boldsymbol{C}, \boldsymbol{D}\) ).

(d) If the dashpot \(b_{2}\) is removed, show that

\[x_{3}=\frac{1}{k_{3}}\left[\left(k_{2}+k_{3}ight) x_{2}-k_{2} x_{1}ight]\]

Choose a new set of independent state variables for this new system and develop the statevariable matrix model (i.e. obtain \(\boldsymbol{A}, \boldsymbol{B}, \boldsymbol{C}, \boldsymbol{D}\) ).

k 000 b m b -000 A f(t) 2 k3 Translational Mechanical System