Repeat Problem 13.18 for the circuit given in Problem 13.13. Assume \(\Delta t=\) \(0.03333 \mathrm{~ms}\).

Data From Problem 13.18:-

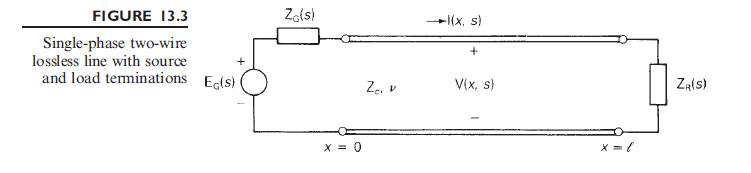
For the circuit given in Problem 13.3, replace the circuit elements by their discretetime equivalent circuits and write nodal equations in a form suitable for computer solution of the sending-end and receiving-end voltages. Give equations for all dependent sources. Assume \(\mathrm{E}=1000 \mathrm{~V}, \mathrm{~L}_{\mathrm{R}}=10 \mathrm{mH}, \mathrm{Z}_{c}=100 \Omega, v=2 \times 10^{8} \mathrm{~m} / \mathrm{s}, l=40 \mathrm{~km}\), and \(\Delta t=0.02 \mathrm{~ms}\).

Data From Problem 13.3:-

Referring to the single-phase two-wire lossless line shown in Figure 13.3, the receiving end is terminated by an inductor with \(\mathrm{L}_{\mathrm{R}}\) henries. The source voltage at the sending end is a step, \(e_{\mathrm{G}}(t)=\mathrm{E} u_{-1}(t)\) with \(\mathrm{Z}_{\mathrm{G}}=\mathrm{Z}_{c}\). Both the line and inductor are initially unenergized. Determine and plot the voltage at the center of the line \(v(l / 2, t)\) versus time \(t\).

Figure 13.3:-

Transcribed Image Text:

FIGURE 13.3 Zo(s) Single-phase two-wire lossless line with source and load terminations Ec(s) x = 0 (x, s) + Ze. v V(x, s) x=l ZR(S)